已知直线 ,一个圆的圆心
,一个圆的圆心 在
在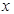 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线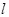 和
和 轴均相切.
轴均相切.
(1)求该圆的方程;
(2)直线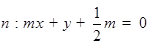 与圆
与圆 交于
交于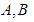 两点,且
两点,且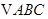 是等边三角形,求
是等边三角形,求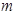 的值.
的值.
已知函数 ,
, .
.
(1)求 的最小正周期;(2)求
的最小正周期;(2)求 的的最大值和最小值;
的的最大值和最小值;
(3)若 ,求
,求 的值.
的值.
已知 ,
, ,求
,求 的值.
的值.
在数列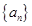 中,
中,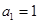 、
、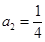 ,且
,且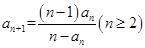 .
.
(Ⅰ) 求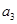 、
、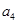 ,猜想
,猜想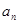 的表达式,并加以证明;
的表达式,并加以证明;
(Ⅱ) 设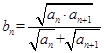 ,求证:对任意的自然数
,求证:对任意的自然数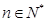 ,都有
,都有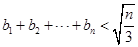 .
.
设椭圆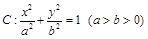 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为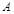 ,离心率为
,离心率为 ,在
,在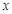 轴负半轴上有一点
轴负半轴上有一点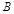 ,且
,且
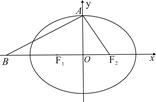
(Ⅰ)若过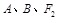 三点的圆恰好与直线
三点的圆恰好与直线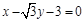 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(Ⅱ)在(Ⅰ)的条件下,过右焦点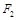 作斜率为
作斜率为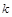 的直线
的直线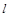 与椭圆C交于
与椭圆C交于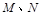 两点,在
两点,在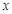 轴上是否存在点
轴上是否存在点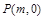 ,使得以
,使得以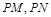 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出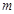 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
如图,四边形ABCD中, 为正三角形,
为正三角形, ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为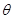 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在 内.
内.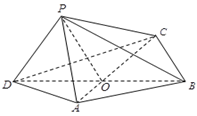
(Ⅰ)求证: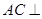 平面PBD;
平面PBD;
(Ⅱ)若已知二面角 的余弦值为
的余弦值为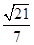 ,求
,求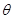 的大小.
的大小.