从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下.观察图形,回答下列问题: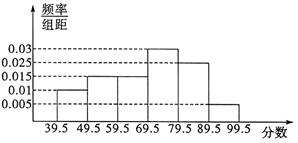
(1)49.5——69.5这一组的频率和频数分别为多少?
(2)估计这次环保知识竞赛成绩的中位数及平均成绩.(精确到小数点后一位)
(本小题满分12分)
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE//平面ABC,平面ACD⊥平面ABC。
(1)求证:DE⊥平面ACD;
(2)若AB=BE=2,求多面体ABCDE的体积。
(本小题满分12分)
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表。
| 序号(i) |
分组(睡眠时间) |
频数(人数) |
频率 |
| 1 |
[4,5) |
6 |
0.12 |
| 2 |
[5,6) |
0.20 |
|
| 3 |
[6,7) |
a |
|
| 4 |
[7,8) |
b |
|
| 5 |
[8,9) |
0.08 |
(1)求n的值.若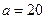 ,将表中数据补全,并画出频率分布直方图.
,将表中数据补全,并画出频率分布直方图.
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求
的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求 的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.
的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.
(本小题满分12分)
在 ,角A,B,C的对边分别为
,角A,B,C的对边分别为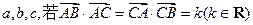 。
。
(1)判断 的形状;
的形状;
(2)若 的值。
的值。
(本小题14分)已知函数 在
在 处取得极值。
处取得极值。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求证:对于区间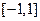 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
;
(Ⅲ)若过点 可作曲线
可作曲线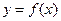 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。
(本小题满分12分)如图所示, 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点的直线l与曲线C相交于不同的两点M、N,问是否存在这样的直线 使
使 与
与 平行,若平行,求出直线
平行,若平行,求出直线 的方程, 若不平行,请说明理由.
的方程, 若不平行,请说明理由.