在某高校自主招生考试中,所有选报II类志愿的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为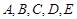 五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为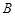 的考生有
的考生有 人.
人.
(1)求该考场考生中“阅读与表达”科目中成绩为 的人数;
的人数;
(2)若等级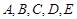 分别对应
分别对应 分,
分,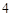 分,
分,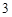 分,
分,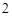 分,
分,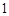 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知在本考场参加测试的考生中,恰有两人的两科成绩均为 .在至少一科成绩为
.在至少一科成绩为 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为 的概率.
的概率.
(本小题满分14分)
已知 是数列
是数列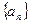 的前
的前 项和,且
项和,且 ,
, 时有
时有 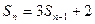 .
.
(1)求证 是等比数列;
是等比数列;
(2)求数列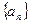 的通项公式.
的通项公式.
(本小题满分14分)已知向量 ,且与向量
,且与向量 的夹角为
的夹角为 ,其中
,其中 是
是 的内角.
的内角.
(1)求角 的大小;(2)求
的大小;(2)求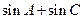 的取值范围.
的取值范围.
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
(本小题满分12分)
已知函数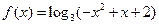 的定义域为集合
的定义域为集合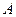 ,
,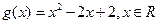 的值域为集合
的值域为集合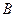 ,
,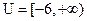 .(1)求
.(1)求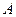 和
和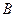 ; (2)求
; (2)求 、
、 .
.
(本小题满分14分)给定函数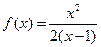
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足,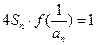 求证:
求证: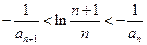 ;
;
(3)设 ,
,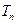 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。