已知椭圆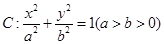
的离心率为
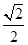，其左，右焦点分别为
，
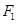，点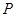
是坐标平面内一点，且
，
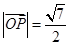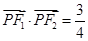，其中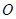
为坐标原点．
（1）求椭圆
的方程；
（2）过点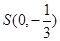
，且斜率为
的动直线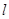
交椭圆于
两点，在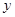
轴上是否存在定点
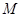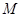，使以为直径的圆恒过这个定点？若存在，求出点的坐标；若不存在，请说明理由．
(本小题满分12分）
椭圆E：
与直线
相交于A、B两点，且OA丄OB(O为坐标原点).
(I)求椭圆E与圆
的交点坐标：
(II)当
时，求椭圆E的方程.
(本小题满分12分）
已知
.
(I )求数列
丨的通项：
(II)若对任意，
〜
恒成立，求c的取值范围.
(本小题满分12分）
如图，直三棱柱
中，AC=BC=1, AAi="3" 
D为CCi上的点，二面角A-A1B-D的余弦值为
(I )求证：CD=2;
(II)求点A到平面A1BD的距离.
(本小题满分12分）
一项试验有两套方案，每套方案试验成功的概率都是
，试验不成功的概率都是
甲随机地从两套方案中选取一套进行这项试验，共试验了 3次，每次实验相互独立，且要从两套方案中等可能地选择一套.
(I)求3次试验都选择了同一套方案且都试验成功的概率：(II)记3次试验中，都选择了第一套方案并试难成功的次数为X,求X的分布列和期望EX.
(本小题满分10分）
'中，三个内角A、B, C的对边分别为a、b、c,且
，
，求