若直线 :
: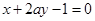 与直线
与直线 :
: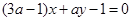 平行,求
平行,求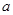 的值.
的值.
设直线
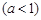 与抛物线
与抛物线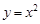 所围成的图形面积为S,它们与直线
所围成的图形面积为S,它们与直线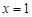 围成的面积为T, 若U=S+T达到最小值,求
围成的面积为T, 若U=S+T达到最小值,求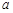 值.
值.
一物体按规律x=bt3作直线运动,式中x为时间t内通过的距离,媒质的阻力正比于速度的平方.试求物体由x=0运动到x=a时,阻力所作的功
分析:
物体A以速度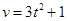 在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以
在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以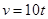 的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s)
的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s)
甲乙两地相距SKm,汽车从甲地匀速行驶到乙地,速度不得超过CKm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成; 可变部分与速度V(Km/h)的平方成正比比例系数为b, 固定成本为a.
(1)把全程运输成本y(元)表示为速度V(km/h)的函数, 并指出这个函数的定义域;
(2)为了使全程运输成本最小; 汽车应以多大的速度行驶.
设工厂A到铁路线的垂直距离为20km, 垂足为B. 铁路线上距离B为100km处有一原料供应站C,现要在铁路BC之间某处D修建一个原料中转站, 再由车站D向工厂修一条公路. 如果已知每千米的铁路运费与公路运费之比为3∶5, 那么D应选在何处, 才能使原料供应站C运货到工厂所需运费最省?