(本小题满分12分)
为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取 名学生进行问卷调查,根据问卷取得了这
名学生进行问卷调查,根据问卷取得了这 名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①
名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组① ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤ ,⑥
,⑥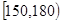 ,⑦
,⑦ ,⑧
,⑧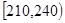 ,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
(1)求 的值并补全下列频率分布直方图;
的值并补全下列频率分布直方图;
(2)如果把“学生晚上学习时间达到两小时”作为是否充分利用时间的标准,对抽取的 名学生,完成下列
名学生,完成下列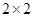 列联表:
列联表:
| |
利用时间充分 |
利用时间不充分 |
总计 |
| 走读生 |
|
|
|
| 住宿生 |
|
10 |
|
| 总计 |
|
|
|
据此资料,你是否认为学生“利用时间是否充分”与走读、住宿有关?
(3)若在第①组、第②组、第⑧组中共抽出3人调查影响有效利用时间的原因,记抽到“学习时间少于60分钟”的学生人数为 ,求
,求 的分布列及期望;
的分布列及期望;
参考公式:

(本题满分12分)
已知函数 .
.
(1)求 的周期和单调递增区间;
的周期和单调递增区间;
(2)说明 的图象可由
的图象可由 的图象经过怎样变化得到.
的图象经过怎样变化得到.
如图,斜率为1的直线过抛物线 的焦点F,与抛物线交于两点A,B,
的焦点F,与抛物线交于两点A,B,
(1)若|AB|=8,求抛物线 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求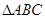 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
已知椭圆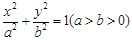 的离心率为
的离心率为 ,且过点(
,且过点( ),
),
(1)求椭圆的方程;
(2)设直线 与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 上的点
上的点 对应的参数
对应的参数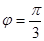 ,射线
,射线 与曲线
与曲线 交于点
交于点 ,
,
(1)求曲线 ,
, 的方程;
的方程;
(2)若点 ,
, 在曲线
在曲线 上,求
上,求 的值.
的值.
已知圆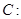
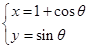 (
(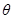 为参数)和直线
为参数)和直线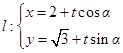 (其中为参数,
(其中为参数,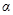 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆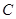 有公共点,求
有公共点,求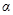 的取值范围.
的取值范围.