已知双曲线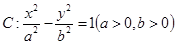 的焦距为
的焦距为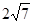 ,其一条渐近线的倾斜角为
,其一条渐近线的倾斜角为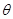 ,且
,且 ,以双曲线
,以双曲线 的实轴为长轴,虚轴为短轴的椭圆为
的实轴为长轴,虚轴为短轴的椭圆为 .
.
(1)求椭圆 的方程;
的方程;
(2)设点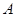 是椭圆
是椭圆 的左顶点,
的左顶点,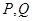 为椭圆
为椭圆 上异于点
上异于点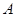 的两动点,若直线
的两动点,若直线 的斜率之积为
的斜率之积为 ,问直线
,问直线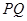 是否恒过定点?若横过定点,求出该点坐标;若不横过定点,说明理由.
是否恒过定点?若横过定点,求出该点坐标;若不横过定点,说明理由.
已知 .求
.求 和
和 的值.
的值.
已知圆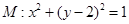 ,设点B,C是直线
,设点B,C是直线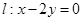 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是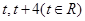 ,点P在线段BC上,过P点作圆M的切线PA,切点为A
,点P在线段BC上,过P点作圆M的切线PA,切点为A
(1)若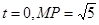 ,求直线
,求直线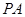 的方程;
的方程;
(2)经过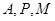 三点的圆的圆心是
三点的圆的圆心是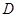 ,求线段
,求线段 (
(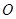 为坐标原点)长的最小值
为坐标原点)长的最小值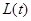
如图,四棱锥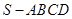 中,
中,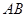 ∥
∥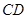 ,
,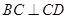 ,侧面
,侧面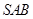 为等边三角形
为等边三角形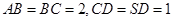
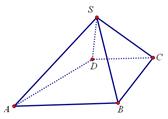
(1)证明: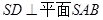
(2)求AB与平面SBC所成角的正弦值
已知:以点C(t,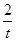 )(t∈R,t≠0)为圆心的圆与
)(t∈R,t≠0)为圆心的圆与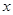 轴交于点O,A,与y轴交于点O,B,其中O为原点
轴交于点O,A,与y轴交于点O,B,其中O为原点
(1)求证:△OAB的面积为定值;
(2)设直线y=–2x+4与圆C交于点M,N,若OM=ON,求圆C的方程
已知圆C: =0
=0
(1)已知不过原点的直线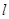 与圆C相切,且在
与圆C相切,且在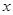 轴,
轴, 轴上的截距相等,求直线
轴上的截距相等,求直线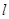 的方程;
的方程;
(2)求经过原点且被圆C截得的线段长为2的直线方程