(1)命题 :“
:“ ”,命题
”,命题 :“
:“ ”,若“
”,若“ 且
且 ”为假命题,求实数
”为假命题,求实数 的取值范围。
的取值范围。
(2)已知 ,
, ,若
,若 是
是 的必要而不充分必要条件,求实数
的必要而不充分必要条件,求实数 的取值范围.
的取值范围.
(本小题满分8分)
实数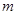 取什么值时,复数
取什么值时,复数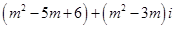 是 (1)实数? (2)虚数?
是 (1)实数? (2)虚数?
(本小题满分8分)
某市居民1999~2003年货币收入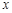 与购买商品支出
与购买商品支出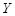 的统计资料如下表所示:
的统计资料如下表所示:
单位:亿元
| 年份 |
1999 |
2000 |
2001 |
2002 |
2003 |
货币收入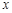 |
40 |
42 |
44 |
47 |
50 |
购买商品支出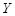 |
33 |
34 |
36 |
39 |
41 |
(Ⅰ)画出散点图,判断x与Y是否具有相关关系;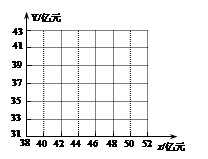
(Ⅱ)已知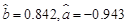 ,请写出Y对x的回归直线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
(本题14分)已知函数, 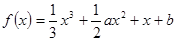
(Ⅰ) 设函数f(x)的图象与x轴交点为A, 曲线y=f(x)在A点处的切线方程是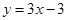 , 求
, 求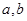 的值;
的值;
(Ⅱ) 若函数 , 求函数
, 求函数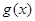 的单调区间.
的单调区间.
(本题共12分)
一盒中放有的黑球和白球,其中黑球4个,白球5个.
(Ⅰ)从盒中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(Ⅲ)若取到白球则停止摸球,求取到第三次时停止摸球的概率
设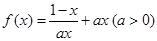 .
.
(Ⅰ)判断函数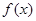 在
在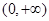 的单调性并证明;
的单调性并证明;
(Ⅱ)求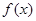 在区间
在区间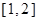 上的最小值。
上的最小值。