某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：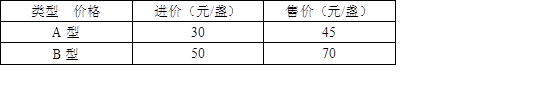
（1）设商场购进A型节能台灯为x盏，销售完这批台灯时可获利为y元，求y关于x的函数解析式；
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
解方程：
（1）2x2﹣32=0
（2）（1+x）2=4
将一次函数y=2x+3的图象平移后过点（1，4），则平移后得到的图象函数关系式为 ．
已知抛物线
的图像经过点O（0，0）A（6，0）。
（1）b = ，c = ；
（2）点B是x正半轴上的一动点，以OB为边在第一象限作一个正方形OBCD，使其一个顶点在抛物线上（不包括B点 ），画出示意图，求点B的坐标；
（3）在（2）的条件下，点E是线段BC上的一个动点，连结DE交线段AC与点F，则线段DF是否存在最小值，如果存在，请求出结果，如果不存在，请说明理由；
如图，⊙O为△ABC的外接圆，直线l与⊙O相切于点P，且l∥BC．要求：仅用无刻度的直尺，在图中画出∠BAC的平分线，并说明理由．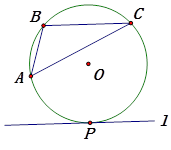
某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出．已知生产x只玩具熊猫的成本为R（元），售价每只为P（元），且R、P与x的关系式分别为R＝500＋30x，P＝170－2x．
（1）当日产量为多少时，每日获得的利润为1750元？
（2）当日产量为多少时，可获得最大利润？最大利润是多少？