如图,在梯形ABCD中,AB∥CD,∠A=90°,CD=4,AB=10, .求BC的长.
.求BC的长.
如图,是由小立方块堆成的几何体,请分别从前面看、左面看和上面看,试将你所看到的平面图形画出来。
a、b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹.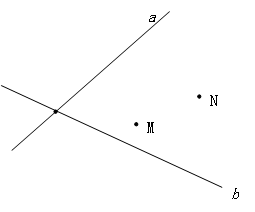
张新和李明相约到丹阳书城去买书,请你根据他们的对话内容(如图),求出李明上次所买书籍的原价。
某公园门票价格规定如下表:
| 购票张数 |
1~50张 |
51~100张 |
100张以上 |
| 每张票的价格 |
13元 |
11元 |
9元 |
某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1240元。问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果(1)班单独组织去游园,作为组织者的你将如何购票才最省钱?