(1)如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.求证:AD=BE.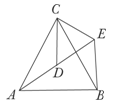
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE边DE上的高,连接BE.
①求证:2CM+BE=AE;
②若将图2中的△DCE绕点C旋转至图3所示位置,①中的结论还成立吗?若不成立,写出它们之间的数量关系.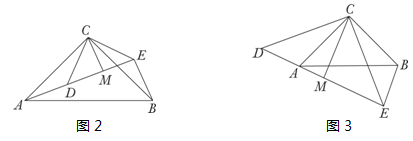
在第一架平衡的天平的左边是“○○△△△”,右边是“■■■■■■■”;第二架天平也平衡,它左边是“○○○△△”,右边是“■■■■■■■■”;第三架天平的左边是“○○○”,右边是“△△△△△”.请问:第三架天平平衡吗?若不平衡,请说出哪边重.
两个数的大小关系可以通过它们的差来判断.若两个数a和b比较大小,则有:当a>b时,一定有a-b>0;当a=b时,一定有a-b=0;当a<b时,一定有a-b<0.反过来也成立,即:当a-b>0时,一定有a>b;当a-b=0时,一定有a=b;当a-b<0时,一定有a<b.因此,我们经常把两个要比较的对象先数量化,再求它们的差,根据差的正、负判断两个对象的大小关系.
根据上述结论,试比较x4+2x2+1与x4+x2+1的大小.
利用不等式的性质解下列不等式,并在数轴上表示解集.
(1)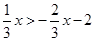 ;
;
(2)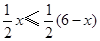 .
.
有甲、乙两种型号的铁丝,每根甲型铁丝长度比每根乙型铁丝少3厘米,现取这两种型号的铁丝各两根分别做长方形的长和宽,焊接成周长大于2.1米的长方形铁丝框.
(1)设每根乙型铁丝长为x厘米,按题意列出不等式.
(2)如果每根乙型铁丝的长度有以下四种选择:45厘米、50厘米、55厘米、58厘米,那么哪些合适?
解不等式5x-12≤2(4x-3),并把解集表示在图的数轴上.