两个数的大小关系可以通过它们的差来判断.若两个数a和b比较大小,则有:当a>b时,一定有a-b>0;当a=b时,一定有a-b=0;当a<b时,一定有a-b<0.反过来也成立,即:当a-b>0时,一定有a>b;当a-b=0时,一定有a=b;当a-b<0时,一定有a<b.因此,我们经常把两个要比较的对象先数量化,再求它们的差,根据差的正、负判断两个对象的大小关系.
根据上述结论,试比较x4+2x2+1与x4+x2+1的大小.
如图,已知直线 过点
过点 和
和 ,
, 是
是 轴正半轴上的动点,
轴正半轴上的动点, 的垂直平分线交
的垂直平分线交 于点
于点 ,交
,交 轴于点
轴于点 .
.
(1)直接写出直线 的解析式;
的解析式;
(2)当 时,设
时,设 ,
, 的面积为
的面积为 ,求S关于t的函数关系式;并求出S的最大值;
,求S关于t的函数关系式;并求出S的最大值;
(3)当点Q在线段AB上(Q与A、B不重合)时,直线 过点A且与x轴平行,问在
过点A且与x轴平行,问在 上是否存在点C,使得
上是否存在点C,使得 是以
是以 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销.商场又用68000元购进第二批这种运动服,所够数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种牌运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?( )
)
已知:如图,⊙O是△ABC的外接圆,AB为⊙O直径,且PA⊥AB于点A,PO⊥AC于点M.
(1)求证: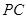 是⊙
是⊙ 的切线;
的切线;
(2)当 ,
, 时,求PC的长.
时,求PC的长.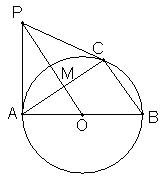
如图,在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
在本学期某次考试中,某校初二⑴、初二⑵两班学生数学成绩统计如下表:
| 分数 |
50 |
60 |
70 |
80 |
90 |
100 |
|
| 人数 |
二(1)班 |
3 |
5 |
16 |
3 |
11 |
12 |
| 二(2)班 |
2 |
5 |
11 |
2 |
13 |
7 |
请根据表格提供的信息回答下列问题:
(1)初二⑴班平均成绩为_________分,初二⑵班平均成绩为________分,从平均成绩看两个班成绩谁优谁次?
(2)二⑴班众数为________分,二⑵班众数为________分。
(3)初二⑴班及格率为_________,初二⑵班及格率为________。
(4)已知二⑴班的方差大于二⑵班的方差,那么说明什么?