如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,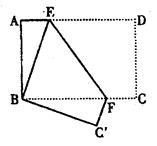
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
(本题满分 分)求下面各式中的
分)求下面各式中的 :
:
(1)
(2)
(本题10分)如图,数轴上的三点A、B、C分别表示有理数a、b、c.(O为原点)
(1)a-b 0,a+c 0,b-c 0.
(用“<”或“>”或“=”号填空)
化简:|a-b|-|a+c|+|b-c|
(2)若数轴上两点A、B对应的数分别为-3、-1,点P为数轴上一动点,其对应的数为x.
①若点P到点A、点B的距离相等,则点P对应的数x为 ;
②若点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以6个单位长
度/秒的速度同时从原点O向左运动.当点A与点B之间的距离为1个单位长度时,求点P所对应的数
x是多少?
(本题6分)为了乘车方便,张强同学买了100元的乘车月票卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y(元)如下表:
| 次数x |
余额y(元) |
| 1 |
100-1.6 |
| 2 |
100-3.2 |
| 3 |
100-4.8 |
| 4 |
100-6.4 |
| … |
… |
(1)写出用乘车的次数x表示余额y的式子;
(2)利用上述式子,帮张强算一算乘了15次车还剩多少元?
(3)张强用100元的乘车月票卡最多乘几次车?
(本题6分)某校图书馆上周借书记录(超过100册的部分记为正,少于100册的部分记为负)如下表:
| 星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| +18 |
-6 |
+15 |
0 |
-12 |
(1)上星期五借出多少册书?
(2)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(3)上星期平均每天借出多少册书?
(本题8分)已知: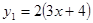 ,
,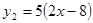 ,当x取何值时
,当x取何值时
(1)y1与y2互为相反数?
(2)y1比y2小2?