有两组卡片，第一组三张卡片上都写着A、B、B，第二组五张卡片上都写着A、B、B、D、E．试用列表法求出从每组卡片中各抽取一张，两张都是B的概率．
（本小题12分）A、B两地相距60千米，甲乙两人分别从A、B两地骑车出发，相向而行，甲比乙迟出发20分钟，每小时比乙多行3千米，在甲出发后1小时40分，两人相遇．问甲乙两人每小时各行多少千米？
若符号“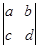
”称为二阶行列式，规定它的运算法则为：
，请你根据上述规定求出下列等式中
的值:
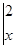
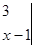=1．
解方程：（1）10-4（x+3）=2(x-1)
（2）
－
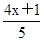＝1
张楠和同学去公园秋游，公园门票5元一张，如果购买20人以上（含20人）的团体票，
可按总票价的八折优惠。
（1）如果张楠他们共有19人，那么买个人票省钱还是买20人一张的团体票省钱？
（2）如果张楠他们买一张20人的团体票，比每人买一张5元的门票总共少花10元，那么张楠他们共有多少人？
如图，一个正五棱柱的底面边长为2cm，高为4cm。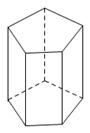
（1）这个棱柱共有多少个面？计算它的侧面积；
（2）这个棱柱共有多少个顶点？有多少条棱？
（3）试用含有
的代数式表示棱柱的顶点数、面数、与棱的条数。