（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．
（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
（3）应用：请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．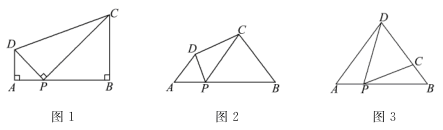
如图，在矩形ABCD中，AC与BD相交于O，∠COD=60°，点E是BC边上的动点，连结DE，OE．
（1）求证：△COD是等边三角形；
（2）如图1，当DE平分∠ADC时，试证明OC=EC，并求出∠DOE的度数；
（3）如图2，当DE平分∠BDC时，试证明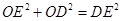
．
如图，在等腰梯形ABCD中，AD∥BC，AB=DC，将腰AB平移至DE的位置时，四边形ABED是平行四边形．
（1）求证：∠C=∠ADE；
（2）若下底BC比上底AD长4cm，DC=3cm，求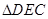
的周长．
已知：如图，点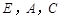
在同一条直线上，
，
．
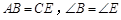求证：
．
在方格图中，每一个小正方形的边长都为1，△ABC的三个顶点都在格点上.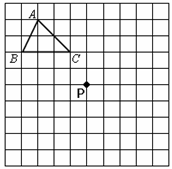
(1)AB的长为；
(2)画出△ABC向下平移4个单位得到的△A1B1C1；
(3)画出△ABC关于点P成中心对称的△A2B2C2.
先化简，再求值：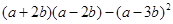
，其中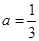
，
．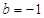