已知椭圆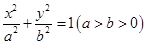 的离心率为
的离心率为 ,点
,点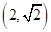 在
在 上.
上.
(1)求 的标准方程;
的标准方程;
(2)设直线 过点
过点 ,当
,当 绕点
绕点 旋转的过程中,与椭圆
旋转的过程中,与椭圆 有两个交点
有两个交点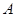 ,
,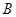 ,求线段
,求线段 的中点
的中点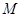 的轨迹方程.
的轨迹方程.
ABCD是梯形,AB∥CD,且AB=2CD,M、N分别是DC和AB的 中点,已知
中点,已知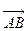 =
=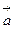 ,
, =
= ,试用
,试用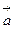 、
、 表示
表示 。
。
O为平面直角坐标系xoy的坐标原点,点A (4,0), B(4,4), C(2,6), 求AC和OB交点P的坐标.
(4,0), B(4,4), C(2,6), 求AC和OB交点P的坐标.
己知A,B,C三点坐标分别为(-1,0),(3,-1),(1,2),并且 .
.
(1)求点E,F的坐标
(2)求证: 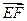 ∥
∥
((本小题满分10分)
选修4—5:不等式选讲 设函数
设函数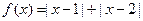
(1)求不等式 的解集;
的解集;
(2)若不等式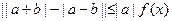 (
( ,
,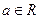 ,
, )恒成立,求实数
)恒成立,求实数 的范围.
的范围.
((本小题满分10分)
选修4—4:坐标系与参数方程
已知直线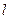 的参数方程为
的参数方程为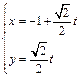 (
(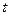 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是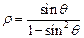 ,以极
,以极 点为原点,极轴为
点为原点,极轴为 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点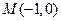 ,直线
,直线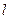 与曲线C交于A、B两点.
与曲线C交于A、B两点.
(1)写出直线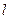 的极坐标方程与曲线C的普通方程;
的极坐标方程与曲线C的普通方程;
(2) 线段MA,MB长度分别记为|MA|,|MB|,求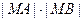 的值.
的值.