((本小题满分10分)
选修4—4:坐标系与参数方程
已知直线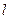 的参数方程为
的参数方程为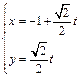 (
(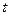 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是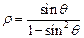 ,以极
,以极 点为原点,极轴为
点为原点,极轴为 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点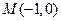 ,直线
,直线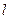 与曲线C交于A、B两点.
与曲线C交于A、B两点.
(1)写出直线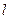 的极坐标方程与曲线C的普通方程;
的极坐标方程与曲线C的普通方程;
(2) 线段MA,MB长度分别记为|MA|,|MB|,求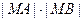 的值.
的值.
(本题12分)在锐角△ABC中,a,b,c分别为角A、B、C所对的边,且 a=2csinA,(1)确定角C的大小;(2)若c=
a=2csinA,(1)确定角C的大小;(2)若c= ,且△ABC的面积为
,且△ABC的面积为 ,求a+b的值。
,求a+b的值。
如图,四边形ABCD是一个边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形小山,其余部分都是平地,P是弧TS上一点,现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.
|
已知b>-1,c>0,函数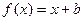 的图象与函数
的图象与函数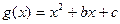 的图象相切.
的图象相切.
(Ⅰ)设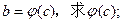
(Ⅱ)是否存在常数c,使得函数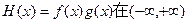 内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
已知函数
(Ⅰ)当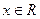 时,求
时,求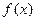 的最小值;
的最小值;
(Ⅱ)若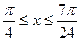 ,求
,求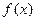 的单调区间。
的单调区间。
在数列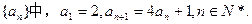
(Ⅰ)证明数列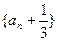 是等比数列;
是等比数列;
(Ⅱ)求数列{ }的前n项和Sn.
}的前n项和Sn.