在等差数列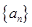 和等比数列
和等比数列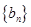 中,
中,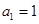 ,
,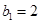 ,
,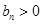 (
(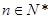 ),且
),且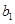 ,
,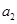 ,
,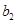 成等差数列,
成等差数列,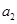 ,
,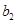 ,
,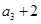 成等比数列.
成等比数列.
(1)求数列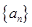 、
、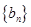 的通项公式;
的通项公式;
(2)设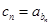 ,数列
,数列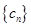 的前
的前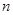 项和为
项和为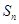 ,若
,若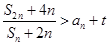 对所有正整数
对所有正整数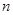 恒成立,求常数
恒成立,求常数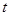 的取值范围.
的取值范围.
已知数列 的前 项和 ,其中 .
(1)证明 是等比数列,并求其通项公式;
(2)若 ,求 .
已知函数 .
(Ⅰ)在图中画出 的图象;
(Ⅱ)求不等式 的解集.

在直角坐标系 中,曲线 的参数方程为 为参数, .在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线 .
(Ⅰ)说明 是哪种曲线,并将 的方程化为极坐标方程;
(Ⅱ)直线 的极坐标方程为 ,其中 满足 ,若曲线 与 的公共点都在 上,求 .
如图, 是等腰三角形, .以 为圆心, 为半径作圆.
(Ⅰ)证明:直线 与 相切;
(Ⅱ)点 , 在 上,且 , , , 四点共圆,证明: .

已知函数 有两个零点.
(Ⅰ)求 的取值范围;
(Ⅱ)设 , 是 的两个零点,证明: .