“十一”黄金周期间，某市风景区在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 人数变化（单位：万人） |
1.6 |
0.8 |
0.4 |
-0.4 |
-0.8 |
0.2 |
-1.2 |
已知9月30日的游客人数为2万人，请回答下列问题：
（1）七天内游客人数最多的是哪天，最少的是哪天？它们相差多少万人？
（2）求这7天的游客总人数是多少万人．
如图，在ΔABC中，∠C=900，延长CA至D，使AD=AB，∠BAC=300，则由图可得cot150的值是（）
A． |
B． |
C． |
D． |
某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了两种优惠办法。
A种办法:卖一支毛笔就赠送一本书法练习本；
B种办法:按购买金额打九折付款。
某校欲为校书法兴趣小组购买这种毛笔10支,书法练习本x(x
)本。
（1）写出每本优惠办法实际付款金额y(元)与x(本)之间的函数关系式；
（2）比较购买同样多的书法练习本时,按那种优惠办法付款更省钱。
如图，已知点A（－6，0），点B和C在y轴正半轴上，∠CAO＝60°，若点B到直线AC的距离是
，求直线AC的解析式和点B的坐标。
从甲、乙两种饮料中各抽取10盒250毫升的果汁饮料，检查其中的维生素C的含量，所得数据如下（单位：毫克）：
甲：120、123、119、121、122、124、119、122、121、119
乙：121、119、124、119、123、124、123、122、123、122
通过计算说明哪种饮料维生素C的含量高？哪种饮料维生素C的含量比较稳定？
某水库的拦水大坝的横截面是个梯形，AD//BC，如图所示。已知斜坡AB的坡度为i =1∶1 ，∠ADC=150º，又AD=20米，AB=28米。求BC的长度。（参考数据：
、
，
）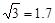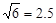