已知集合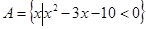 ,
, .
.
(1)当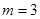 时,求集合
时,求集合 ,
,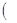 ∁
∁ ;
;
(2)若 ,求实数
,求实数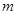 的取值范围.
的取值范围.
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ADE沿直线DE翻折成△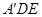 ,使平面
,使平面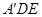 ⊥平面BCDE,F为线段
⊥平面BCDE,F为线段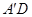 的中点.
的中点.
(Ⅰ)求证:EF∥平面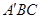 ;
;
(Ⅱ)求直线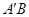 与平面
与平面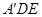 所成角的正切值.
所成角的正切值. 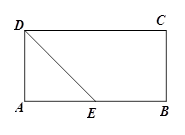
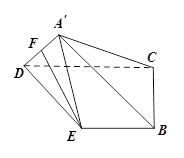
在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.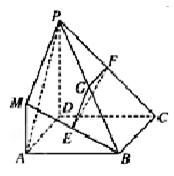
(1)求证:平面EFG⊥平面PDC;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.
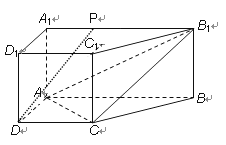
如图所示,直棱柱 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
(1)求证: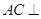 平面
平面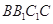 ;
;
(2)在A1B1上是否存一点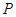 ,使得
,使得 与平面
与平面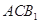 平行?证明你的结论.
平行?证明你的结论.
如图,平面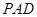 ⊥平面
⊥平面 ,
, 为正方形,
为正方形, 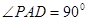 ,且
,且 分别是线段
分别是线段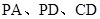 的中点.
的中点.
(Ⅰ)求证: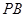 //平面
//平面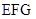 ;
;
(Ⅱ)求异面直线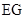 与
与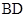 所成角的余弦值.
所成角的余弦值.
如图, 在空间四边形SABC中, 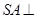 平面ABC,
平面ABC, 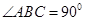 ,
, 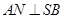 于N,
于N, 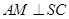 于M.
于M.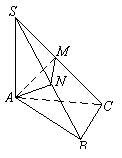
求证:①AN^BC; ②平面SAC^平面ANM