已知函数
(1)当 时,求函数
时,求函数 的最小值和最大值
的最小值和最大值
(2)设三角形角 的对边分别为
的对边分别为 且
且 ,
, ,若
,若 ,求
,求 的值.
的值.
已知函数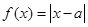
(I)若不等式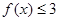 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(II)在(I)的条件下,若 对一切实数
对一切实数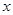 恒成立,求实数
恒成立,求实数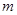 的取值范围.
的取值范围.
在直角坐标系 中,圆
中,圆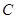 的参数方程
的参数方程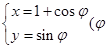 为参数).以
为参数).以 为极点,
为极点,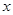 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆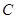 的极坐标方程;
的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是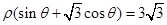 ,射线
,射线 与圆
与圆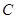 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段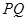 的长.
的长.
设函数 ,其中
,其中 为常数。
为常数。
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数 有极值点,求
有极值点,求 的取值范围及
的取值范围及 的极值点。
的极值点。
已知椭圆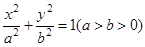 的离心率为
的离心率为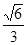 ,且过点
,且过点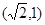 .
.
(1)求椭圆的方程;
(2)若过点C(-1,0)且斜率为 的直线
的直线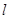 与椭圆相交于不同的两点
与椭圆相交于不同的两点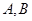 ,试问在
,试问在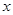 轴上是否存在点
轴上是否存在点 ,使
,使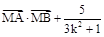 是与
是与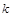 无关的常数?若存在,求出点
无关的常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.