如图，在三棱锥P-ABC中，
．
（1）求证：平面PBC⊥平面PAC；
（2）若PA=1，AB=2，BC=
，在直线AC上是否存在一点D，使得直线BD与平面PBC所成角为30°？若存在，求出CD的长；若不存在，说明理由．
设椭圆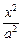
+
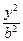=1(a＞b＞0)的左焦点为F1(－2,0),左准线l1与x轴交于点N(－3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
(1)求直线l和椭圆的方程；
(2)求证:点F1(－2,0)在以线段AB为直径的圆上.
设点A(－2，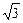
)，椭圆
+ 
=1的右焦点为F，点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是多少？
椭圆
+ 
=1的焦点为F1、F2，点P为其上的动点，当∠F1PF2为钝角时，点P横坐标的取值范围是？
点M到一个定点F(0，2)的距离和它到一条定直线y=8的距离之比是1∶2，则M点的轨迹方程是？
已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.