( 本小题满分12分)
本小题满分12分)
某公司为了实现2011年10 00万元利润的目标,准备制定一个激励销售人员的奖励方案:
00万元利润的目标,准备制定一个激励销售人员的奖励方案:
销售利润达到10万元时,按销售利润进行奖励,且奖金数额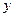 (单位:万元)随销售利润
(单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的
(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的 ,现有三个奖励模型:
,现有三个奖励模型: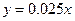 ,
,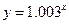 ,
, ,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据:
,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据: )
)
(本小题满分12分)
已知矩形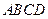 的对角线交于点
的对角线交于点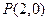 ,边
,边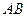 所在直线的方程为
所在直线的方程为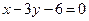 ,点
,点 在边
在边 所在的直线上,
所在的直线上,
(1)求矩形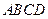 的外接圆的方程;
的外接圆的方程;
(2)已知直线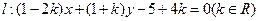 ,求证:直线
,求证:直线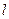 与矩形
与矩形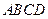 的外接圆恒相交,并求出相交的弦长最短时的直线
的外接圆恒相交,并求出相交的弦长最短时的直线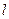 的方程.
的方程.
(本小题满分12分)
已知向量m ,n
,n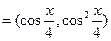 ,函数
,函数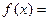 m·n.
m·n.
(1)若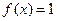 ,求
,求 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是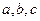 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分15分)
已知函数
(1)求 的单调区间;
的单调区间;
(2)若 ,
, ,求
,求 的取值范围.
的取值范围.
(本小题满 分15分)
分15分)
已 知椭圆
知椭圆 的离心率
的离心率 ,过点
,过点
 和
和
 的直线与原点的距离为
的直线与原点的距离为 .
.
(1)求椭圆的方程;
(2)设 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过 作直线交椭圆于
作直线交椭圆于
 、
、 两点,求
两点,求 的内切圆半径
的内切圆半径 的最大值.
的最大值.