已知函数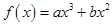
，
在点
处的切线方程为
．
（1）求函数的解析式；
（2）若对任意的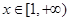
，
恒成立，求实数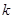
的取值范围．
某种产品的广告费用支出
(百万)与销售额
(百万)之间有如下的对应数据:
|
2 |
4 |
5 |
6 |
8 |
|
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10(百万)时,销售收入的值.
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
性别与看营养说明列联表单位: 名
| 男 |
女 |
总计 |
|
| 看营养说明 |
50 |
 |
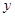80 |
| 不看营养说明 |
 |
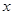20 |
30 |
| 总计 |
60 |
50 |
 |
(1)根据以上表格,写出
的值.
(2)根据以上列联表，问有多大把握认为“性别与在购买食物时看营养说明”有关？
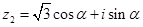已知复数
,
,求复数
实部的最值.
已知数列{an}满足a1＝2，an＋1＝an－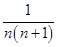
.
(1)求数列{an}的通项公式；
(2)设bn＝nan·2n，求数列{bn}的前n项和Sn
已知函数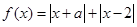
（1）当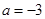
时，求不等式
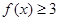的解集；
（2）若
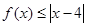在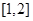
上恒成立，求
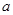的取值范围。