已知函数 ,
, ,其中
,其中
(Ⅰ)求 在
在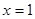 处的切线方程;
处的切线方程;
(Ⅱ)当 时,证明:
时,证明:
 .
.
一个机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如下:
如果y与x线性相关,求回归直线方程.
一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组对应数据:
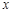 |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
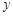 |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
判断它们是否有相关关系.
(本题满分14分)设有关于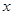 的一元二次方程
的一元二次方程 .
.
(1)若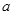 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若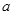 是从区间[0,3]任取的一个数,
是从区间[0,3]任取的一个数, 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
(本题满分14分)已知圆 和圆外一点
和圆外一点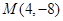 .
.
(1)过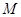 作圆的割线交圆于
作圆的割线交圆于 两点,若|
两点,若| |=4,求直线
|=4,求直线 的方程;
的方程;
(2)过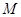 作圆的切线,切点为
作圆的切线,切点为 ,求切线长及
,求切线长及 所在直线的方程.
所在直线的方程.
(本题满分13分)在正三角形 内有一动点
内有一动点 ,已知
,已知 到三顶点的距离分别为
到三顶点的距离分别为 ,且满足
,且满足 ,求
,求 点的轨迹方程.
点的轨迹方程.