如图所示,质量 ,电阻
,电阻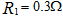 ,长度
,长度 的导体棒
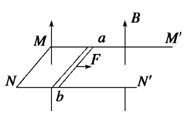
的导体棒 横放在U型金属框架上.框架质量
横放在U型金属框架上.框架质量 ,放在绝缘水平面上,与水平面间的动摩擦因数
,放在绝缘水平面上,与水平面间的动摩擦因数 ,相距
,相距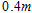 的
的 相互平行,电阻不计且足够长.电阻
相互平行,电阻不计且足够长.电阻 的
的 垂直于
垂直于 .整个装置处于竖直向上的匀强磁场中,磁感应强度
.整个装置处于竖直向上的匀强磁场中,磁感应强度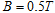 .垂直于
.垂直于 施加
施加 的水平恒力,
的水平恒力, 从静止开始无摩擦地运动,始终与
从静止开始无摩擦地运动,始终与 保持良好接触.当
保持良好接触.当 运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力,
运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力, 取
取 .
.
(1)求框架开始运动时 速度
速度 的大小;
的大小;
(2)从 开始运动到框架开始运动的过程中,
开始运动到框架开始运动的过程中, 上产生的热量
上产生的热量 ,求该过程
,求该过程 位移
位移 的大小。
的大小。
已知X光子的能量为0.6 MeV,在康普顿散射后,波长变化了20%,求反冲电子的能量.
在康普顿散射中,如果反冲电子的速度为光速的60%,则因散射使电子获得能量是静能的几倍?
人们发现光电效应具有瞬时性和对各种金属都存在极限频率的规律.请问谁提出了何种学说很好地解释了上述规律?已知锌的逸出功为3.34 eV,用某单色紫外线照射锌板时,逸出光电子的最大速度为106 m/s,求该紫外线的波长λ.(电子质量me=9.11×10-31 kg,普朗克常量h=6.63×10-34 J·s,1 eV=1.60×10-19 J)
在半径r="10" m的球壳中心有一盏功率为P="40" W的钠光灯(可视为点光源),发出的钠黄光的波长为λ="0.59" μm,已知普朗克常量h=6.63×10-34 J·s,真空中光速c=3×108 m/s.试求每秒钟穿过S="1" cm2球壳面积的光子数目.
已知金属铯的极限波长为0.66 μm,用0.05 μm的光照射铯金属表面,发射光电子的最大初动能为多少?铯金属的逸出功为多少?