在半径r="10" m的球壳中心有一盏功率为P="40" W的钠光灯(可视为点光源),发出的钠黄光的波长为λ="0.59" μm,已知普朗克常量h=6.63×10-34 J·s,真空中光速c=3×108 m/s.试求每秒钟穿过S="1" cm2球壳面积的光子数目.
如图所示,AOB是光滑水平轨道,BC是半径为R的1/4光滑圆弧轨道,两轨道恰好相切,质量为M的小木块静止在O点,一质量为m(m = M/9)的子弹以某一初速度水平向右射入小木块内不穿出,木块恰好滑到圆弧的最高点C处(子弹、小木块均可看成质点)问:(1)子弹射入木块之前的速度? (2)若每当小木块在O点时,立即有相同的子弹以相同的速度射入小木块,并留在其中,当第6颗子弹射入小木块后,小木块沿圆弧上升的高度是多大?(3)当第n颗子弹射入小木块后,小木块沿圆弧能上升的最大高度为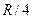 时,则n值是多少?
时,则n值是多少?
宇航员在某一星球上以速度v0竖直向上抛出一个小球,经过时间t,小球又落回到抛出点.然后他用一根长为L的细绳把一个质量为m的小球悬挂在O点,使小球处于静止状态.现在最低点给小球一个水平向右的冲量I,使小球能在竖直平面内运动,若细绳在小球运动过程中始终处于拉紧状态,则冲量I应满足什么条件?
如果赤道附近的两个居民用卫星电话通过同步卫星转发的无线电信号与对方通话,则在讲完话后,最短要等多少时间才能听到对方的回话?已知地球的质量为M,地球半径为R,万有引力常量为G,地球的自转周期为T,无线电信号的传播速度为c(最后答案用题目中的符号表示).
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电粒子从P点沿半径方向向左侧射出,最终打到Q点,不计粒子的重力。求:
(1)粒子从P点到Q点的最短运动时间及其对应的运动速率;
(2)符合条件的所有粒子的运动时间及其对应的运动速率。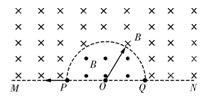
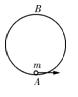
宇航员抵达半径为R的星球表面后,做了如下的实验:取一竖直光滑圆轨道,一质量为m的物体以一定的初速度在竖直平面内做完整的圆周运动,如图所示。测量出当物体运动到圆周的最高点B位置时,物体对轨道的压力为F1;经过最低点A时,物体对轨道的压力为F2。已知引力常量为G,试根据题中所提供的条件和测量结果,求:(不考虑星球的自转)
(1)该星球表面的重力加速度;
(2)该星球的质量M。