如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC, 过点A作AC的垂线交CN于点P.
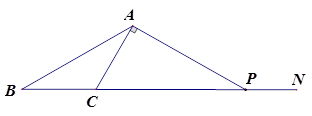
(1)若∠APC=30°,求证:AB=AP;
(2)若AP=8,BP=16,求AC的长;
(3)若点P在BC的延长线上运动,∠APB的平分线交AB于点M.你认为∠AMP的大小是否发生变化?若变化,请说明理由;若不变化,求出∠AMP的大小.
按要求解下列两个方程:
(1)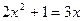 (配方法)(2)
(配方法)(2)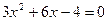 (公式法)
(公式法)
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量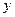 (件)与销售单价
(件)与销售单价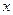 (元)符合一次函数关系:
(元)符合一次函数关系:
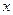 |
… |
60 |
65 |
70 |
75 |
80 |
… |
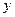 |
… |
60 |
55 |
50 |
45 |
40 |
… |
(1)求销售量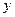 与销售单价
与销售单价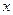 的函数关系式;
的函数关系式;
(2)若该商场获得利润为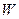 元,试写出利润
元,试写出利润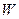 与销售单价
与销售单价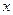 之间的关系式;并求出销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;并求出销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价的范围.
如图12-1,已知直线y= -x+4交x轴于点A,交y轴于点B.
(1)写出A、B两点的坐标分别是:;
(2)设点P是射线y = x(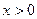 )上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
)上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
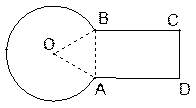
如图9,一种零件的横截面由三角形、矩形、扇形组成,其中∠BOA=60°,AD=25mm,半径AO=10mm,求该零件的横截面积.
图9
如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形