已知在长方形ABCD中,AB=4,BC=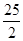 ,O为BC上一点,BO=
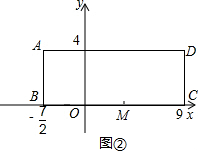
,O为BC上一点,BO= ,如图所示,以BC所在直线为x轴,O为坐标原点建立平面直角坐标系,M为线段OC上的一点.
,如图所示,以BC所在直线为x轴,O为坐标原点建立平面直角坐标系,M为线段OC上的一点.
(1)若点M的坐标为(1,0),如图①,以OM为一边作等腰△OMP,使点P在长方形ABCD的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P的坐标;
(2)若将(1)中的点M的坐标改为(4,0),其它条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P的坐标;
(3)若将(1)中的点M的坐标改为(5,0),其它条件不变,如图③,请直接写出符合条件的等腰三角形有几个?请直接写出所有符合条件的点P的坐标.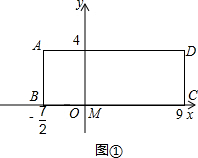

如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,
沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m,求路灯杆AB的高度.
在平原上,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=-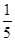 x2+10x.
x2+10x.
(1)经过多长时间,炮弹达到它的最高点?最高点的高度是多少?
(2)经过多长时间,炮弹落在地上爆炸?
如图,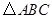 在方格纸中
在方格纸中
(1)请在方格纸上建立平面直角坐标系,使 ,并求出B点坐标;
,并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将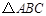 放大,画出放大后的图形
放大,画出放大后的图形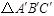 ;
;
(3)计算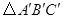 的面积
的面积 .
.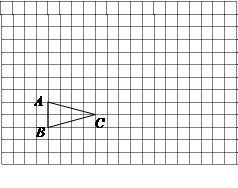
①解方程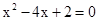
②计算:
题满分12分)在平面直角坐标系中,动点P到点S(1,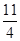 ),与过T点(0,
),与过T点(0,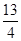 )且平行于x轴的直线距离相等,设点P的坐标为(x,y)
)且平行于x轴的直线距离相等,设点P的坐标为(x,y)
(1)试求出y与x函数关系式;
(2)设点P运动到x轴上时为点A、B(点A在点B的左边),运动到最高点为点C;动动到y轴上时为点D;求出A、B、C、D四点的坐标;
(3)在(2)的条件下,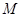 为线段
为线段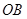 (点O为坐标原点)上的一个动点,过
(点O为坐标原点)上的一个动点,过 轴上一点
轴上一点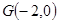 作
作 的垂线,垂足为
的垂线,垂足为 ,直线
,直线 交
交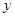 轴于点
轴于点 ,当
,当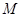 点在线段
点在线段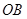 上运动时,现给出两个结论: ①
上运动时,现给出两个结论: ①  ②
② ,其中有且只有一个结论是正确的,请你判断哪个结论正确,并证明.
,其中有且只有一个结论是正确的,请你判断哪个结论正确,并证明.