定义：如果
，那么称
为
的劳格数，记为
．
（1）根据劳格数的定义，可知：
那么：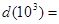
．
（2）劳格数有如下运算性质：
若
为正数，则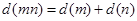
;
．
根据运算性质，填空：
＝ ，
若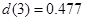
，则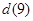
＝ ，
＝ ．
（3）下表中与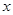
数对应的劳格数
有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
|
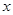1．5 |
3 |
5 |
6 |
8 |
9 |
12 |
27 |
|
 |
 |
 |
 |
 |
 |
 |
 |
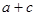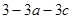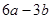如图，直线y=x+3与坐标轴分别交于A、B两点，抛物线
经过点A、B，顶点为C，连结CB并延长交x轴于点E，点D与点B关于抛物线的对称轴MN对称。
（1）求抛物线的解析式及顶点C的坐标；
（2）求证：四边形ABCD是直角梯形。
为了对学生进行爱国主义教育，某校组织学生去看演出。有甲乙两种票，已知甲乙两种票的单价比为4：3，单价和为42元。
（1）甲、乙两种票的单价分别是多少元？
（2）学校计划拿出不超过750元的资金，让七年级一班的36名学生首先观看，且规定购买甲种票必须多于15张，有哪几种购买方案？
在一副扑克牌中，拿出红桃2、红桃3、红桃4、红桃5四张牌，小明从中随机摸出一张记下牌面上的数字为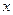
，然后放回洗匀，再由小华随机摸出一张，记下牌面上的数字为
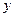，组成一对数（，）。
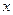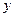（1）用列表法或树状图表示出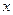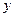（，）的所有可能出现的结果；
（2）求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率。
如图，点D在双曲线上，AD垂直
轴，垂足为
A，点C在AD上，CB平行于轴交双曲线于点B，直线AB与
轴交于点F，已知AC：
AD=1：3，点C的坐标为（2，2）。
（1）求该双曲线的解析式；
（2）求△OFA的面积。
益趣玩具店购进一种儿童玩具，计划每个售价
36元，能盈利80﹪，在销售中出现了滞销，于是先后两次降价，售价降为25元。
（1）求这种玩具的进价。
（2）求平均每次降价的百分率（精确到0.1﹪）