益趣玩具店购进一种儿童玩具，计划每个售价
36元，能盈利80﹪，在销售中出现了滞销，于是先后两次降价，售价降为25元。
（1）求这种玩具的进价。
（2）求平均每次降价的百分率（精确到0.1﹪）
某支股票上周末的收盘价格是10.00元，本周一到周五的收盘情况如下表：（“＋”表示股票比前一天上涨，“－”表示股票比前一天下跌）
| 上周末收盘价 |
周一 |
周二 |
周三 |
周四 |
周五 |
| 10.00 |
＋0.28 |
－2.36 |
＋1.80 |
－0.35 |
＋0.08 |
（1）周一至周五这支股票每天的收盘价各是多少元? （ 5分）
（2）本周末的收盘价比上周末收盘价是上涨了，还是下跌了多少?
（3）这五天的收盘价中哪天的最高?哪天的最低?相差多少?
某车间有技术工85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配 一套，问加工甲、乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套？
将一批工业最新动态信息输入管理储存网络，甲独做需6小时，乙独做需4小时，甲先做30分钟，然后甲、乙一起做，则甲、乙一起做还需多少小时才能完成工作？
已知：如图B，C两点把线段AD分成2∶5∶3三部分，M为AD的中点，BM=6cm，求CM和AD的长．
如果方程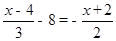
的解与方程4x－（3a+1）=6x+2a－1的解相同，求式子a－
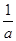的值.