如图,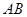 是圆台上底面圆
是圆台上底面圆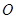 的直径,
的直径,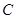 是圆
是圆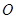 上不同于
上不同于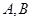 的一点,
的一点,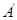 是下底面圆
是下底面圆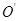 上一点,过
上一点,过 的截面垂直与下底面,
的截面垂直与下底面,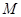 为
为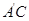 的中点,又
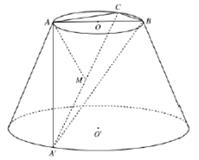
的中点,又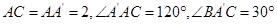 .
.
(1)求证: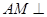 平面
平面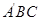 ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知函数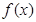 是定义在
是定义在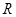 上的偶函数.若
上的偶函数.若 时,
时,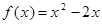 .
.
(Ⅰ)当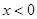 时,求函数
时,求函数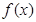 的解析式;
的解析式;
(Ⅱ)画出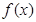 的简图;(要求绘制在答题卷的坐标纸上);
的简图;(要求绘制在答题卷的坐标纸上);
(Ⅲ)结合图像写出 的单调区间(只写结论,不用证明).
的单调区间(只写结论,不用证明).
(本小题满分12分)已知函数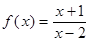 ,其中
,其中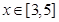 .
.
(Ⅰ)用定义证明函数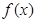 在
在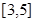 上单调递减;
上单调递减;
(Ⅱ)结合单调性,求函数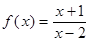 在区间
在区间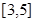 上的最大值和最小值.
上的最大值和最小值.
(本小题满分10分)已知集合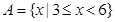 ,
,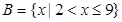 .
.
(Ⅰ)求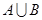 ,
,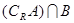 ;
;
(Ⅱ)已知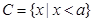 ,若
,若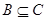 ,求实数
,求实数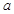 的取值范围.
的取值范围.
(本题满分14分)数列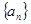 中,
中,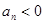 , 前n项和
, 前n项和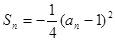 .
.
(1)求数列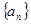 的通项公式;
的通项公式;
(2)设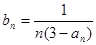 (
(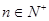 ),
),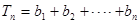 ,若对任意
,若对任意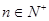 ,总存在
,总存在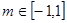 使
使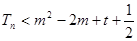 成立,求出t的取值范围.
成立,求出t的取值范围.
(本题满分13分) 如图,已知四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
, ,
, ,
, 平面
平面 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)若 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.