有一个容量为100的某校毕业生起始月薪的样本数据的分组及各组的频数如下:
| 起始月薪(百元) |
[13,14) |
[14,15) |
[15,16) |
[16,17) |
[17,18) |
[18,19) |
[19,20) |
[20,21] |
| 频数 |
7 |
11 |
26 |
23 |
15 |
8 |
4 |
6 |
(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)根据频率分布估计该校毕业生起始月薪低于2000元的频率.
已知抛物线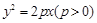 的焦点为
的焦点为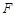 ,点
,点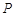 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,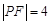 .
.
(1)求抛物线的方程;
(2)设点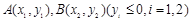 是抛物线上的两点,
是抛物线上的两点,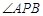 的角平分线与
的角平分线与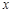 轴垂直,求
轴垂直,求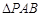 的面积最大时直线
的面积最大时直线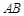 的方程.
的方程.
已知函数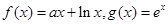 .
.
(1)当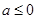 时,求
时,求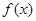 的单调区间;
的单调区间;
(2)若不等式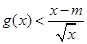 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(3)证明:当a=0时,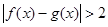 .
.
如图,在三棱锥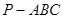 中,直线
中,直线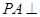 平面
平面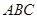 ,且
,且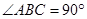 ,又点
,又点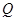 ,
,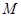 ,
, 分别是线段
分别是线段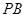 ,
,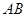 ,
,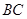 的中点,且点
的中点,且点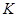 是线段
是线段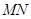 上的动点.
上的动点.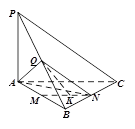
(1)证明:直线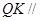 平面
平面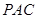 ;
;
(2)若 ,求二面角
,求二面角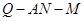 的平面角的余弦值.
的平面角的余弦值.
设数列 的前
的前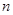 项和为
项和为 ,
,
已知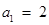 ,
, ,
, ,
,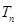 是数列
是数列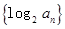 的前
的前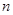 项和.
项和.
(1)求数列 的通项公式;(2)求
的通项公式;(2)求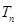 ;
;
(3)求满足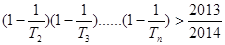 的最大正整数
的最大正整数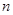 的值.
的值.
已知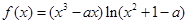 (
(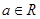 )
)
(1)若方程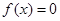 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得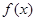 在
在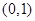 上恰有两个极值点
上恰有两个极值点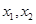 ,且满足
,且满足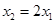 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.