如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.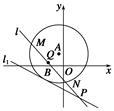
(1)求圆A的方程;
(2)当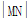 =2
=2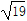 时,求直线l的方程;
时,求直线l的方程;
(3)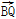 ·
· 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
在某种工业品的生产过程中,每日次品数 与每日产量
与每日产量 的函数关系式为
的函数关系式为 ,该工厂售出一件正品可获利
,该工厂售出一件正品可获利 元,但生产一件次品就损失
元,但生产一件次品就损失 元,为了获得最大利润,日产量应定为多少?
元,为了获得最大利润,日产量应定为多少?
有一块三角形的铁板余料,如图1所示.已知 .工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算水箱的高为多少时,水箱的容积最大?最大容积是多少?
.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算水箱的高为多少时,水箱的容积最大?最大容积是多少?
已知函数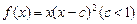 在区间
在区间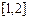 上的最小值为4,求
上的最小值为4,求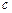 的值.
的值.
已知函数 的导数
的导数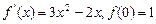 .求函数
.求函数 在区间
在区间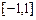 上的最小值与最大值.
上的最小值与最大值.
将数列
中的所有项按每一行比上一行多一项的规则排成下表:
……
记表中的第一列数
……构成的数列为
,
,
为数列
的前
项和,且满足
(I)证明数列
成等差数列,并求数列
的通项公式;
(II)上表中,若从第三行起,每一行中的数从左到右的顺序均构成等比数列,且公比为同一个正数,当
时,求上表中第
行所有项的和