已知椭圆 :
:
 的离心率
的离心率 ,原点到过点
,原点到过点 ,
, 的直线的距离是
的直线的距离是 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线 与两定直线
与两定直线 和
和 分别交于
分别交于 两点.若直线
两点.若直线 总与椭圆
总与椭圆 有且只有一个公共点,试探究:
有且只有一个公共点,试探究: 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
已知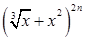 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x- )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以 ,
, 为边的平行四边形的面积;
为边的平行四边形的面积;
(2)若|a|= ,且a分别与
,且a分别与 ,
, 垂直,求向量a的坐标.
垂直,求向量a的坐标.
已知函数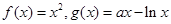 ,
,
(1)若函数 在
在 上是减函数,求实数
上是减函数,求实数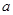 的取值范围;
的取值范围;
(2)是否存在实数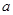 ,当
,当 (
(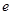 是自然常数)时,函数
是自然常数)时,函数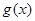 的最小值是3,若存在,求出
的最小值是3,若存在,求出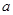 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当 时,证明:
时,证明: .
.
设函数 .
.
(1)若曲线 在点
在点 处与直线
处与直线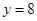 相切,求a,b的值;
相切,求a,b的值;
(2)求函数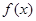 的单调区间.
的单调区间.
如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
(1)求出体积V与高h的函数关系式并指出其定义域;
(2)问当 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?