如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
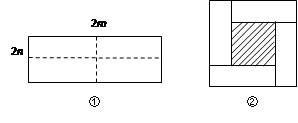
(1)你认为图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积,
方法① .方法② .
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
如图,已知直线PA交⊙O于A.B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CDPA⊥,垂足为D. 
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
如图,平行四边形ABCD中, ,点
,点 的坐标是
的坐标是 ,以点
,以点 为顶点的抛物线
为顶点的抛物线 经过
经过 轴上的点
轴上的点 .
.
(1)求点 的坐标;
的坐标;
(2)若抛物线向上平移后恰好经过点 ,求平移后抛物线的解析式.
,求平移后抛物线的解析式.
已知:如图,AB是⊙O的直径,点C.D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
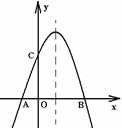
如图,抛物线的对称轴是直线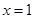 ,它与
,它与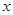 轴交于
轴交于 ,
,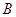 两点,与
两点,与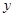 轴交于
轴交于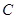 点,点
点,点 ,
,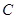 的坐标分别是
的坐标分别是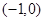 ,
,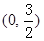 .
.
(1) 求此抛物线对应的函数解析式;
(2) 若点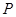 是抛物线上位于
是抛物线上位于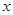 轴上方的一个动点,求△ABP面积的最大值.
轴上方的一个动点,求△ABP面积的最大值.
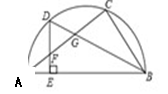
如图,△ABC内接于半圆,AB为直径,设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
求证:FD=FG.