2014年11月10日APEC会议在北京召开，某服务部需从大学生中招收志愿者，被招收的志愿者需参加笔试和面试两部分，把参加笔试的60名大学生按成绩分组：第1组[75，80）有3人，第2组[80，85）有21人，第3组[85，90）有18人，第4组[90，95）有12人，第5组[95，100）有6人
（1）现决定在笔试成绩较高的第3、4、5组中用分层抽样抽取12人进行面试，则第3、4、5组各抽取多少人？
（2）已知甲和乙的成绩均在第5组，在（1）的条件下，求甲、乙至少有1人进入面试的概率．
已知函数
.
（1）若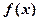
在实数集R上单调递增，求实数
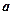的取值范围；
（2）设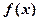在区间（2,3）中至少有一个极值点，求实数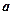的取值范围.
（本小题满分12分）
如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD=AB=2，E是PB的中点，F是AD的中点．
⑴求异面直线PD与AE所成角的大小；
⑵求证：EF⊥平面PBC ；
⑶求二面角F—PC—B的大小．
（本小题满分12分）
根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3. 设各车主购买保险相互独立.
（1）求该地1位车主至少购买甲、乙两种保险中的一种的概率；
（2）求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
（本小题满分12分）
在四边形ABCD中，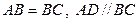
,且
，沿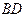
将其折成一个二面角
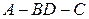，使
.
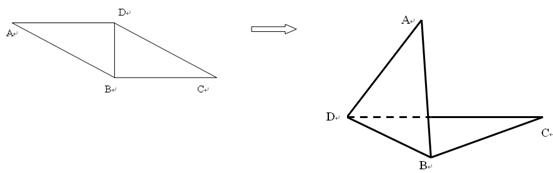
（1）求折后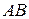
与平面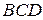
所成的角的余弦值；
（2）求折后点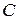
到平面
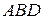的距离.
（本小题满分12分）
已知函数
在
处有极小值
.
(1)求函数
的单调区间;
(2)求函数在闭区间
上的最大值和最小值.