如图，抛物线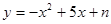
经过点A（1，0），与y轴交于点B．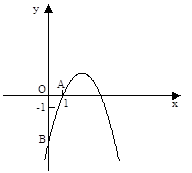
（1）求抛物线的解析式；
（2）P是y轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标．将抛物线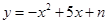
沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点．
我们知道：任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零．由此可得：如果ax+b=0，其中a、b为有理数，x为无理数，那么a=0且b=0．运用上述知识，解决下列问题：
（1）如果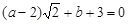
，其中a、b为有理数，那么
=，
=；
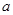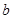（2）如果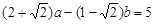
，其中a、b为有理数，求
的值．
（1）
（2）
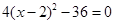
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
（2）阅读下面的内容，并解决后面的问题：
如图2，AP、CP分别平分∠BAD、∠BCD，
若∠ABC=36°，∠ADC=16°，求∠P的度数；
解：∵AP、CP分别平分∠BAD、∠BCD∴∠1=∠2，∠3=∠4，
由（1）的结论得：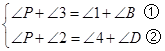
，
①+②，得2∠P+∠2+∠3=∠1+∠4+∠B+∠D．
∴∠P=
（∠B+∠D）=26°．
① 如图3， 直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，求∠P的度数；
② 在图4中，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．
③ 在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．（本题8分）
随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场．一水果经销商购进了A、B两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：
有两种配货方式（整箱配货）
方案一：甲乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；
方案二：按照甲乙两店盈利相同配货，其中A种水果甲店箱，乙店箱，B种水果甲店箱，乙店箱
（1）如果按照方案一配货，请你计算出经销商能盈利多少元；
（2）请你将方案二填写完整（只写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多．（本题6分）
先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式
解：∵
∴可化为 
；
由有理数的乘法法则“两数相乘，同号得正”，得①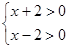
或②
；
解不等式组①，得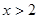
，解不等式组②，得
，
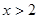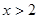∴的解集为或，即一元二次不等式的解集为或；
（1）一元二次不等式
的解集为；
（2）分式不等式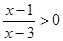
的解集为；
（3）解一元二次不等式
；