“端午”节前，第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干，放入不透明的盒中，此时随机取出火腿粽子的概率为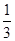
；妈妈发现小亮喜欢吃的火腿粽子偏少，第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中，这时随机取出火腿粽子的概率为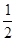
（1）请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只？
（2）若妈妈从盒中取出火腿粽子6只、豆沙粽子7只送爷爷和奶奶后，再让小亮从盒中不放回地任取2只，问恰有火腿粽子、豆沙粽子各1只的概率是多少？
如图EF∥AD，∠1=∠2，∠BAC="70" o，求∠AGD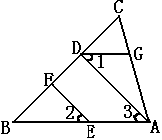
证明：∵EF∥AD，（已知）
∴∠2="" .（）
又∵∠1=∠2，（已知）
∴∠1=∠3.（等量代换）
∴AB∥（）
∴∠BAC+="180" o .（
）.
∵∠BAC="70" o
∴∠AGD="" .
如图，平移三角形ABC，使点A移动到点D,画出平移后的三角形DEF。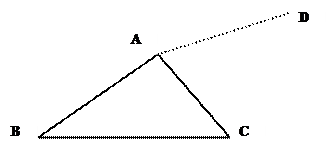
如图所示，直线AB, CD相交于点O, P是直线CD上一点。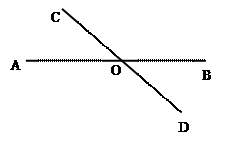
①过点P画直线AB的垂线段PE;
②过点P画直线CD的垂线，与直线AB相交于F点；
③说明线段PE, PO, FO三者的大小关系，其依据是什么？
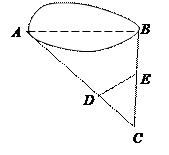
如图，零件的外径为16cm，要求它的壁厚x，需要先求出内径AB，现用一个交叉钳(AD与BC相等)去量，若测得OA
︰OD=OB︰OC=3︰1，CD＝5cm，你能求零件的壁厚x吗？
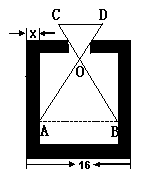
如图，点D、E分别在AC、BC上，如果测得CD＝20m，CE＝40m，AD=100m，BE
=20m，DE=45m,求A、B两地间的距离。