【实际情境】
某中学九年级学生步行到郊外春游．一班的学生组成前队，速度为4km/h，二班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时，后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12km/h．
【数学研究】
若不计队伍的长度，如图，折线A-B-C、A-D-E分别表示后队、联络员在行进过程中，离前队的路程y（km）与后队行进时间x（h）之间的部分函数图象．
（1）求线段AB对应的函数关系式；
（2）求点E的坐标，并说明它的实际意义；
（3）联络员从出发到他折返后第一次与后队相遇的过程中，当x为何值时，他离前队的路程与他离后队的路程相等？
.
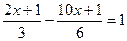.用一副三角板，可以画出那些度数的角？
合并同类项:
,并求当x=2，y=1时，代数式的值.
（本小题满分6分）
端午节吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只粽子：一
只
肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同。小明喜欢
吃红枣馅的粽子。
（1）请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率；
（2）在吃粽子之前，小明准备用一格均匀的正四面体骰子（如图所示）
进行吃粽子的模拟试验，规定：掷得点数1向上代表肉馅，点数2向上代
表香肠馅，点数3，
向上代表红枣馅，连续抛掷这个骰子两次表示随机
吃两只粽子，从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗？试说明理由。
（本小题满分6分）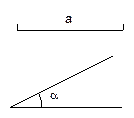
（1）画图，已知线段a和锐角
，求作Rt△ABC，使它的一边为a，一锐角为（不写作法，要保留作图痕迹，作出其中一个满足条件的直角三角形即可）。
（2）回答问题：
1满足上述条件的大小不同的共有种。
|
2若＝
，求最大的Rt△ABC的面积。