如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.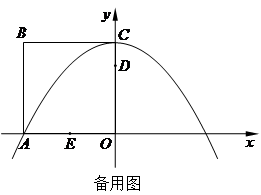
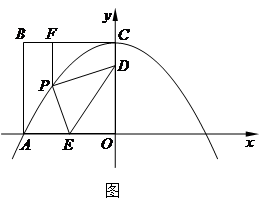
(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,
①请直接写出所有“好点”的个数,
②如果使△PDE的周长最小的点P也是一个“好点”,请求出△PDE的周长最小时“好点”的坐标.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在个点上,在建立平面直角坐标系后,点A的坐标为(﹣6,1),点B的坐标为(﹣3,1),点C的坐标为(﹣3,3).
(1)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出的图形Rt△A1B1C1,并写出点A1的坐标;
(2)将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形.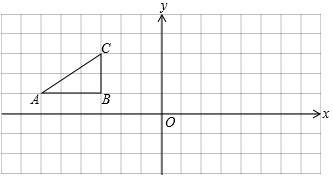
在平面直角坐标系中,点M的坐标为(a,﹣2a).
(1)当a=﹣1时,点M在坐标系的第 二 象限;(直接填写答案)
(2)将点M向左平移2个单位,再向上平移1个单位后得到点N,当点N在第三象限时,求a的取值范围.
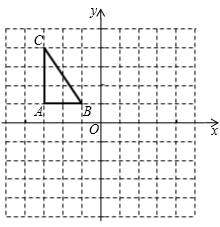
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)作出△ABC向左平移5格后得到的△A1B1C1;
(2)作出△ABC关于点O的中心对称图形△A2B2C2;
(3)求△A1B1C1的面积.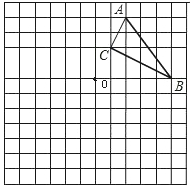
作图题:在方格纸中,将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.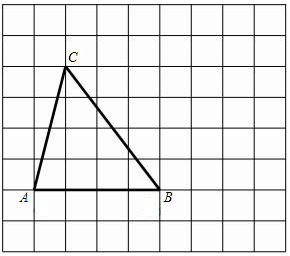
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移4个单位后,得到△A1B1C1,请画出△A1B1C1,并直接写出点C1的坐标.
(2)作出△A1B1C1关于x轴的对称图形△A2B2C2,并直接写出点A2的坐标.
(3)请由图形直接判断以点C1、C2、B2、B1为顶点的四边形是什么四边形?并求出它的面积.