某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元,请比较哪种方案的最大利润更高,并说明理由。
已知实数m,n(m>n)是方程 的两个根,求
的两个根,求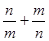 的值.
的值.
初二(3)班文艺委员小兰同学在布置“庆国庆、迎奥运”联欢会现场时,想从一块长为20cm,宽为8cm的长方形彩色纸板上剪下一个腰长为10cm的等腰三角形,并使其一个顶点在长方形的一边上,另两个顶点落在对边上,请你帮她设计出符合要求的等腰三角形,并求出等腰三角形的底边长. (本小题6分 )
已知:
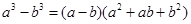
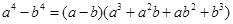 ;按此规律,则:
;按此规律,则:
(1)
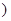 ;
;
(2)若 ,请你能根据上述规律求出代数式
,请你能根据上述规律求出代数式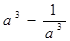 的值(本小题5分 )
的值(本小题5分 )
为了美化校园,学校准备在三边长分别是 和
和 的两块三角形空地上种植花草,你能分别计算出这两块空地的面积吗?如果能请写出你的计算过程。
的两块三角形空地上种植花草,你能分别计算出这两块空地的面积吗?如果能请写出你的计算过程。
(本小题5分 )
①数轴上的点并不都表示有理数,如图以数轴的单位长度为边作正方形,以数轴上的原点O为圆心,正方形的对角线的长为半径作弧与数轴交于一点A,则点A表示的数为这种说明问题的方式体现的数学思想方法叫做()
| A.代入法 | B.换元法 | C.数形结合 | D.分类讨论 |
②请你模仿上面的例子在下面的数轴上找出表示 的点:(本小题5分 )
的点:(本小题5分 )