如图所示是家用电瓶车充电器对蓄电池组进行充电的电路。A、B两端接在充电机的输出端上,蓄电池组的内阻r=2Ω,指示灯L的规格为“6V,3W”。当可变电阻R调到20Ω时,指示灯恰能正常发光,电压表示数为52V(设电压表内阻极大),试求:
(1)充电机的输出功率;
(2)对蓄电池组的输入功率;
(3)蓄电池组的总电动势;
(4)充电机的充电效率。
电动机的额定电压是220V,额定功率是2.2kW,线圈的电阻是1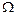 ,当电动机正常工作时,求:
,当电动机正常工作时,求:
(1)1s时间内线圈上产生的热量是多少?
(2)1s时间内转化的机械能有多少?
一小圆盘静止在一长为L的薄滑板上,且位于滑板的中央,滑板放在水平地面上,如图所示。已知盘与滑板间的动摩擦因数为μ1,盘与地面间的动摩擦因数为μ2。现突然以恒定的加速度a(a>μ1 g),使滑板沿水平地面运动,加速度的方向是水平的且向右。若水平地面足够大,则小圆盘从开始运动到最后停止共走了多远?(以g表示重力加速度)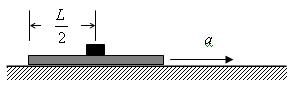
如图,原长分别为L1和L2,劲度系数分别为k1和k2的轻质弹簧竖直地悬挂在天花板上,两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态。现用一个质量为m的平板把下面的物体竖直地缓慢地向上托起,直到两个弹簧的总长度等于两弹簧原长之和,这时托起平板竖直向上的力是多少?m2上升的高度是多少?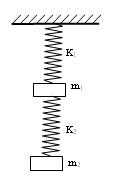
甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持10m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机,需在接力区前适当的位置设置标记。在某次练习中,甲在接力区前S0=15m处作了标记,并以V=10m/s的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒。已知接力区的长度为L=20m。
求:(1)此次练习中乙在接棒前的加速度a;
(2)在完成交接棒时乙离接力区末端的距离。
如图,原长分别为L1和L2,劲度系数分别为k1和k2的轻质弹簧竖直地悬挂在天花板上,两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态。现用一个质量为m的平板把下面的物体竖直地缓慢地向上托起,直到两个弹簧的总长度等于两弹簧原长之和,这时托起平板竖直向上的力是多少?m2上升的高度是多少?