已知抛物线 ,焦点为
,焦点为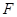 ,准线为
,准线为 ,抛物线
,抛物线 上一点
上一点 的横坐标为3,且点
的横坐标为3,且点 到准线
到准线 的距离为5.
的距离为5.
(1)求抛物线 的方程;
的方程;
(2)若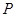 为抛物线
为抛物线 上的动点,求线段
上的动点,求线段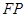 的中点
的中点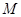 的轨迹方程.
的轨迹方程.
如图18图,已知AA1//BB1//CC1,且AA1=BB1=2CC1=2,AA1⊥面A1B1C1,△A1B1C1是边长为2的正三角形,M为BC的中点。
(1)求证:MA1⊥B1C1;
(2)求二面角C1—MB1—A1的平面角的正切值。
甲乙两人进行象棋比赛,规定:每次胜者得1分,负者得0分;当其中一人的得分比另一人的得分多2分时则赢得这场比赛,此时比赛结束;同时规定比赛的次数最多不超过6次,即经6次比赛,得分多者赢得比赛,得分相等为和局。已知每次比赛甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求:
(1)ξ=2的概率;
(2)随机变量ξ的分布列及数学期望。
已知函数
(1)当 时,求函数
时,求函数 的最小正周期;
的最小正周期;
(2)若函数 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围。
的取值范围。
已知椭圆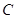 的中心在原点,一个焦点
的中心在原点,一个焦点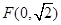 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是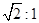 .若椭圆
.若椭圆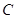 在第一象限的一点
在第一象限的一点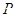 的横坐标为1,过点
的横坐标为1,过点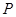 作倾斜角互补的两条不同的直线
作倾斜角互补的两条不同的直线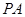 ,
, 分别交椭圆
分别交椭圆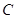 于另外两点
于另外两点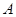 ,
, .
.
(Ⅰ)求椭圆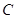 的方程;
的方程;
(Ⅱ)求证:直线 的斜率为定值;
的斜率为定值;
(Ⅲ)求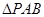 面积的最大值.
面积的最大值.
已知函数 .
.
(1)当 时,求函数
时,求函数 的最小值;
的最小值;
(2)若 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.