用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩下的3支签中任意抽出1支签。
(1)用树状图或列表格等方法列出所有可能出现的结果;
(2)求抽出的两支签中,1支为甲签、1支为丁签的概率。
在“全民读书月活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图.请根据相关信息,解答下列问题:(直接填写结果)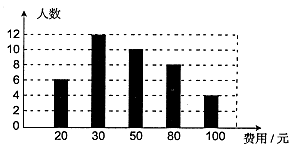
(1)这次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
解方程和不等式组:
(1)
(2)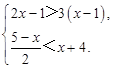
先化简,再求值: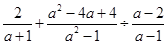 ,其中
,其中
如图1,在平面直角坐标系 内,已知点
内,已知点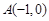 ,
,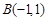 ,
,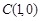 ,
, ,记线段
,记线段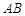 为
为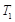 ,线段
,线段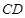 为
为 ,点
,点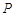 是坐标系内一点.给出如下定义:若存在过点
是坐标系内一点.给出如下定义:若存在过点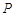 的直线l与
的直线l与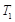 ,
, 都有公共点,则称点
都有公共点,则称点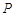 是
是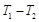 联络点.
联络点.
例如,点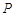
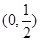 是
是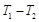 联络点.
联络点.
(1)以下各点中,__________________是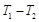 联络点(填出所有正确的序号);
联络点(填出所有正确的序号);
①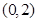 ;②
;② 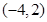 ;③
;③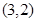 .
.
(2)直接在图1中画出所有 联络点所组成的区域,用阴影部分表示;
联络点所组成的区域,用阴影部分表示;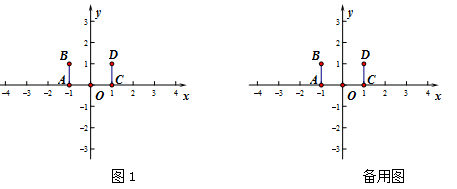
(3)已知点M在y轴上,以M为圆心,r为半径画圆,⊙M上只有一个点为 联络点,①若
联络点,①若 ,求点M的纵坐标;
,求点M的纵坐标;
②求 的取值范围.
的取值范围.