已知:定义在R上的函数 ,对于任意实数a, b都满足
,对于任意实数a, b都满足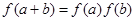 ,且
,且 ,网当
,网当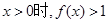 .
.
(Ⅰ)求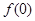 的值;
的值;
(Ⅱ)证明 在
在 上是增函数;
上是增函数;
(Ⅲ)求不等式 的解集.
的解集.
函数 .
.
(1)求函数 的极值;
的极值;
(2)设函数 ,对
,对 ,都有
,都有 ,求实数m的取值范围.
,求实数m的取值范围.
已知a>0,且 .设命题
.设命题 :函数
:函数 在(0,+∞)上单调递减,命题
在(0,+∞)上单调递减,命题 :曲线
:曲线 与x轴交于不同的两点,如果
与x轴交于不同的两点,如果 是假命题,
是假命题, 是真命题,求a的取值范围.
是真命题,求a的取值范围.
已知椭圆的两个焦点坐标分别是 ,
, ,并且经过点
,并且经过点 ,求它的标准方程.
,求它的标准方程.
设函数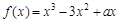
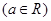 .
.
(1)当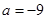 时,求函数
时,求函数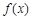 的极大值;
的极大值;
(2)若函数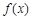 的图象与函数
的图象与函数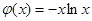 的图象有三个不同的交点,求
的图象有三个不同的交点,求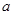 的取值范围;
的取值范围;
(3)设 ,当
,当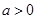 时,求函数
时,求函数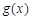 的单调减区间.
的单调减区间.
如图所示,在平面直角坐标系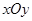 中,设椭圆
中,设椭圆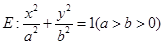 ,其中
,其中 ,过椭圆
,过椭圆 内一点
内一点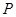
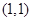 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 和
和 ,且满足
,且满足 ,
,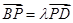 ,其中
,其中 为正常数. 当点
为正常数. 当点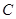 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的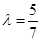 .
.
(1)求椭圆 的离心率;
的离心率;
(2)求 与
与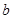 的值;
的值;
(3)当 变化时,
变化时,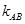 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.