已知集合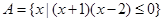 ,
,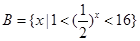 ,
, .
.
(1)求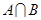 ;
;
(2)如果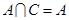 ,求实数
,求实数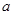 的取值范围.
的取值范围.
(、(本题12分)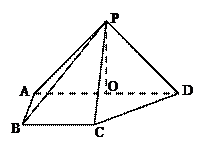
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ,底面ABCD为直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC="2," O为AD中点.
,底面ABCD为直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC="2," O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求直线PB与平面PA D所成角的正弦值;
D所成角的正弦值;
(3)线段AD上是否存在点Q,使得三棱锥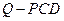 的体积为
的体积为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本题12分)
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
(1)求证: 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
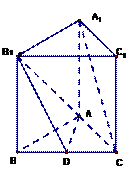
(本题12分)如图,在直三棱柱(侧棱与底面垂直的三棱柱) 中,
中,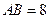 ,
, ,
, ,
, 是
是 边的中点.
边的中点.
(Ⅰ)求证: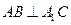 ;
;
(Ⅱ)求证: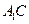 ∥面
∥面 .
.
(本题12分)已知函数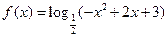 (1)求
(1)求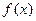 的定义域;(2)求
的定义域;(2)求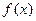 的值域。
的值域。
本题12分)已知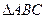 的顶点
的顶点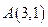 ,
,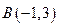
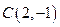 求:(1)
求:(1)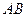 边上的中线所在的直线方程(2)
边上的中线所在的直线方程(2)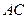 边上的高
边上的高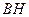 所在的直线方程.
所在的直线方程.