先化简,再求值:(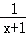 +
+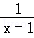 )÷
)÷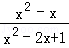 ,其中x=
,其中x=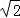 ﹣1
﹣1
解方程.
(1)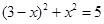
(2)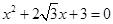
在 中,
中,  分别为
分别为 所对的边,我们称关于
所对的边,我们称关于 的一元二次方程
的一元二次方程 为“
为“ 的☆方程”.根据规定解答下列问题:
的☆方程”.根据规定解答下列问题:
(1)“ 的☆方程”
的☆方程” 的根的情况是(填序号);①有两个相等的实数根;②有两个不相等的实数根;③没有实数根.
的根的情况是(填序号);①有两个相等的实数根;②有两个不相等的实数根;③没有实数根.
(2)如图, 为⊙
为⊙ 的直径,点
的直径,点 为⊙
为⊙ 上的一点,
上的一点, 的平分线交⊙
的平分线交⊙ 于点
于点 ,
,
求“ 的☆方程”
的☆方程” 的解;
的解;
(3)若 是“
是“ 的☆方程”
的☆方程” 的一个根,其中
的一个根,其中 均为正整数,且
均为正整数,且 ,求:①求
,求:①求 的值;②求“
的值;②求“ 的☆方程”的另一个根.
的☆方程”的另一个根.
用适当的方法解下列方程.
(1)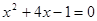
(2)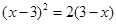
按要求解答下列各小题。
(1)计算:6cos60°-(sin21°-1)0×5tan45°;
(2)解方程:4x(3x-2)=6x-4.