爱动脑筋的小明在学习了全等三角形和等腰三角形有关知识后作了如下探索:
(1)已知,如图,△ABC中,∠BAC是锐角,AB=AC,高AD、BG 所在的直线相交于点H, 且AG=BG,则AH和BC的关系是:_____________________;

(2)若把(1)中的“∠BAC是锐角”改为“∠BAC是钝角”(如图2),其他条件都不变, AH和BC的关系是否仍然成立, 若成立,请在图2中用三角板和量角器画出完整的图形并证明;若不成立,请说明理由.
(年黑龙江齐齐哈尔、大兴安岭地区、黑河10分)某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
(年黑龙江牡丹江农垦10分)某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.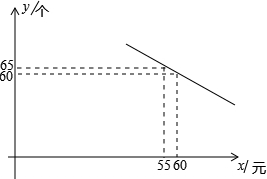
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
(年贵州黔西南12分)已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式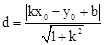 计算.
计算.
例如:求点P(﹣2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x﹣y+1=0,其中k=1,b=1.
所以点P(﹣2,1)到直线y=x+1的距离为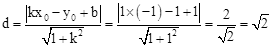 .
.
根据以上材料,求:
(1)点P(1,1)到直线y=3x﹣2的距离,并说明点P与直线的位置关系;
(2)点P(2,﹣1)到直线y=2x﹣1的距离;
(3)已知直线y=﹣x+1与y=﹣x+3平行,求这两条直线的距离.
(年贵州黔南10分)已知某厂现有A种金属70吨,B种金属52吨,现计划用这两种金属生产M、N两种型号的合金产品共80000套,已知做一套M型号的合金产品需要A种金属0.6kg,B种金属0.9kg,可获利润45元;做一套N型号的合金产品需要A种金属1.1kg,B种金属0.4kg,可获利润50元.若设生产N种型号的合金产品大数为x,用这批金属生产这两种型号的合金产品所获总利润为y元.
(1)求y与x的函数关系式,并求出自变量x的取值范围;
(2)在生产这批合金产品时,N型号的合金产品应生产多少套,该厂所获利润最大?最大利润是多少?
(年贵州黔东南12分)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.