【问题背景】如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE ≌△AFG,从而得出结论:___________________.
【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
【结论应用】如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏东60°的A处,舰艇乙在指挥中心南偏西20°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正南方向以40海里/小时的速度前进,舰艇乙沿南偏东40°的方向以50海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
在平面直角坐标系 中,函数 的图象 经过点 ,直线 与图象 交于点 ,与 轴交于点 .
(1)求 的值;
(2)横、纵坐标都是整数的点叫做整点.记图象 在点 , 之间的部分与线段 , , 围成的区域(不含边界)为 .
①当 时,直接写出区域 内的整点个数;
②若区域 内恰有4个整点,结合函数图象,求 的取值范围.
如图, 是 的直径,过 外一点 作 的两条切线 , ,切点分别为 , ,连接 , .
(1)求证: ;
(2)连接 , ,若 , , ,求 的长.

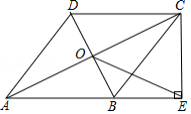
如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 .
(1)求证:四边形 是菱形;
(2)若 , ,求 的长.
关于 的一元二次方程 .
(1)当 时,利用根的判别式判断方程根的情况;
(2)若方程有两个相等的实数根,写出一组满足条件的 , 的值,并求此时方程的根.
下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线 及直线 外一点 .
求作:直线 ,使得 .

作法:如图,
①在直线 上取一点 ,作射线 ,以点 为圆心, 长为半径画弧,交 的延长线于点 ;
②在直线 上取一点 (不与点 重合),作射线 ,以点 为圆心, 长为半径画弧,交 的延长线于点 ;
③作直线 .所以直线 就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明: , ,
(填推理的依据).